Демонстрационный эксперимент является одним из важнейших методов обучения физике, как в средней, так и в высшей школе. Являясь, согласно педагогической науке, средством наглядности, он способствует организации восприятия учащимися и студентами учебного материала, его пониманию и запоминанию, способствует повышению интереса к изучению физики, созданию мотивации учения. Однако организация на современном уровне натурного демонстрационного эксперимента, как в средней, так и в высшей школе, связана с серьёзными финансовыми затратами, в результате чего существенно повышается значение виртуального демонстрационного эксперимента в учебном процессе и он начинает постепенно вытеснять реальный эксперимент. Нужно отметить, что причины актуализации применения виртуального лабораторного эксперимента в средней школе были подробно проанализированы в трудах Богатыревой Ю.И., Шахаевой Д.В. [5]. Эти же причины, имеющие место и при изучении курса общей физики в педагогическом вузе, обсуждались авторами статьи в публикации «О применении виртуального демонстрационного и лабораторного эксперимента по физике в высшей школе» [1]. В настоящей работе на конкретном примере рассматриваются методические аспекты комплексного подхода к организации лекционного демонстрационного эксперимента, используемого авторами в учебном процессе и заключающегося в сочетании натурного и виртуального экспериментов.
Лекционный демонстрационный эксперимент является одной из важнейших составляющих обучения физике. Традиционно такая демонстрация проводится на заранее подготовленной экспериментальной установке и иллюстрирует базовые положения той или иной теории. Однако, как правило, объяснение опыта даётся на качественном уровне без детального количественного анализа, так как за исключением простейших опытов, такое рассмотрение представляется достаточно сложным. Кроме того, такой подход требует тщательной предлекционной подготовки со стороны преподавателя, что в современных условиях при росте нагрузки и сокращении аудиторных часов представляет определённую проблему. Наконец, необходимо присутствие студента в аудитории, что в реальности тоже не всегда выполняется, а для заочного и дистанционного образования вообще не достижимо.
Наличие компьютерной и мультимедийной техники позволяет до определённой степени решить эту проблему. Реальный эксперимент готовится один раз, выполняется в наиболее подходящих условиях, записывается на видео, обрабатывается и монтируется с помощью видеоредактора, коих великое множество, в том числе и бесплатных, и выкладывается на официальной странице сайта кафедры. Заметим, что для выполнения этой работы можно и весьма желательно привлекать самих студентов в рамках самостоятельной работы, выполнения курсовых или ВКР. Опыт, поставленный своими руками, надолго останется в памяти и вызовет больше доверия со стороны сокурсников. Примеры таких экспериментов можно посмотреть на странице кафедры общей и теоретической физики (
http://tsput.ru/res/fizika/VIDEO_1/index_v.htm). Далее эту запись можно использовать, как во время лекции, так и дать на неё ссылку для самостоятельного просмотра и изучения, причём, в домашних абсолютно безопасных условиях с многократным повторением.
Устные, вмонтированные в видео, или размещённые по известным студентам адресу комментарии дают качественное объяснение эксперимента.
Следующий этап – это количественное описание. Аналитическое решение чаще всего бывает достаточно длинным, а иногда и невозможным, поэтому необходимо привлечение компьютерных средств моделирования физических процессов, таких как известные среды математической обработки или схемотехнического моделирования, или авторских программ, например [4]. Следует отметить, что натурный эксперимент и его количественный анализ могут быть разнесены во времени и пространстве, что создаёт дополнительные удобства для студента.
Заметим, что количественное описание позволяет глубже понять физику процесса, а также выявить детали, которые могут ускользнуть при качественном рассмотрении.
В качестве примера рассмотрим одну из возможных демонстраций по движению заряженных частиц в магнитном поле и действию силы Лоренца. Подобный эксперимент, основанный на движении электролита в скрещенных электрическом и магнитном полях, описан в учебнике под редакцией В.И. Ивероновой (1972) [9, С. 372], а его натурных реализаций, разной степени качества и наглядности, можно немало найти на просторах Интернета [7,8].
Основная часть. 1. Реальный эксперимент 1. В опыте, выполненном авторами [6], применено простое, широко распространённое и безопасное оборудование: стандартные подковоообразные магниты, дистиллированная вода, поваренная соль (NaCl), чашка Петри, перманганат калия для хорошей визуализации, низковольтный источник постоянного тока, проволока для электродов.
Качественное объяснение эксперимента достаточно простое и может быть использовано при изучении соответствующих тем не только в ВУЗе, но и в школе. Ионы, разогнанные электрическим полем, под действием магнитного поля начинают двигаться по искривлённым, на первый взгляд, круговым или спиральным траекториям, передают свой импульс всей массе электролита, и тот приходит во вращательное движение.
Таким образом, первый этап демонстрационного эксперимента выполнен полностью.
Однако количественное описание представляется достаточно сложным, и поэтому практически нигде не приводится. Кроме того, при такой постановке затруднён ряд измерений, а, следовательно, сравнение теории и эксперимента весьма проблематично. Количественные оценки, приведённые в статье авторов «Демонстрация и моделирование движения заряженных частиц в магнитном и электрическом полях» [2], также носят скорее качественный характер.
2. Реальный эксперимент 2. Авторами был выполнен более удачно подготовленный эксперимент, и в настоящей публикации будет проведено его подробное количественное рассмотрение.
Экспериментальная установка представляет собой коаксиальные цилиндрические электроды, приклеенные термоклеем к плоскому основанию (см. рис. 1), пространство между которыми заполнено раствором медного купороса CuSO4 в дистиллированной воде. Концентрация раствора составляла 2,2 г на 20 мл воды. Электроды изготовлены из латуни толщиной 0,25 мм. Их высота 9 мм, диаметры и, соответственно, радиусы d1=32 мм, r1=16 мм,d2=57 мм, r2=28,5 мм, радиус средней линии =22,25 мм, полурасстояние между электродами =6,25 мм. Неравномерность зазора между электродами около 2 мм. Высота раствора b=4÷5 мм, следовательно, все размеры сравнимы и ни о каких предельных случаях речь не идёт.
Источником магнитного поля, перпендикулярного плоскости рисунка, является постоянный цилиндрический магнит от старого динамика большого диаметра 74 мм, расположенный снизу (на рис.1 не показан).
Схема опыта, а также силы, действующие на ионыCu+2и SO4-2, образующиеся при диссоциации молекул медного купороса, со стороны электрического и магнитного полей, показаны на рис. 2 и рис. 3, соответственно.


Для разгона частиц электроды подключаются к стабилизированному источнику питания БП-2, напряжение на выходе которого составляет 5 В. Использование источника ВС-4-12 нежелательно, так как реально он даёт пульсирующий ток. Для демонстрации и её качественного описания это неважно, однако для количественных расчётов может сыграть существенную роль, так что зависимость полей от времени лучше устранить.
Период обращения определялся непосредственно наблюдением за мелкими частицами на поверхности электролита. Для этого многократно с помощью секундомера засекается время N оборотов частицы. Затем определяется среднее значение периода. Естественно, что при этом допускается немалая погрешность. Результаты эксперимента приведены в следующей таблице.

3. Уравнения движения. Для количественного описания будем исходить из уравнений движения
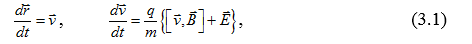
где q – заряд частицы, m– её масса, – индукция магнитного поля, – напряжённость электрического поля. Вязкость среды не учитываем.
Рассматриваем плоский случай, цилиндрическую (полярную) геометрию и симметричные поля.
Тогда уравнения движения принимают вид
, 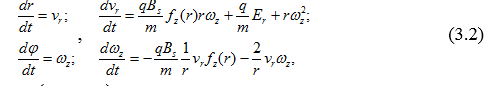
где vr – радиальная (лучевая) скорость, – угловая скорость, r и – полярные координаты, функция определяет радиальную неоднородность магнитного поля: , если магнитное поле мы принимаем однородным, и в случае неоднородного поля.
Если ввести обозначения -  циклотронная частота, взятая со своим знаком (её знак определяется знаком заряда частицы q),
циклотронная частота, взятая со своим знаком (её знак определяется знаком заряда частицы q), 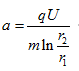 - параметр, характеризующий электрическое поле, то система уравнений (3.2) принимает вид
- параметр, характеризующий электрическое поле, то система уравнений (3.2) принимает вид
, 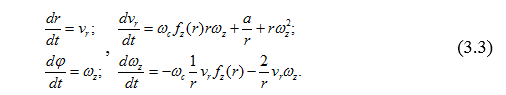
Эти уравнения дополняются достаточно очевидными начальными условиями
. 
4. Численные расчёты и результаты. Для расчёта траекторий заряженных частиц в магнитных полях достаточно сложных конфигураций авторами написана программа [2], подробное описание которой дано в [3].
Моделирование данного эксперимента проводилось в приложении PTC Math Cad, которое очень хорошо приспособлено для подобных задач. Изучаемые функции записываются практически в общепринятой нотации, все параметры легко изменяются, результаты могут быть выведены графически.
Фрагмент подготовленного рабочего листа представлен на рис. 4 и рис. 5. Расчёты проведены для положительных и отрицательных двухзарядных ионов при напряжении U = 0,2 В (опыт 1 из таблицы) и завышенном в 2 раза магнитном поле Bs = 54 мТл (о причинах такого завышения в дальнейшем будет дано соответствующее пояснение).
На этих рисунках: внешняя и внутренняя окружности – электроды, пунктирная окружность между ними – начальный (средний) радиус, кривые 1 и 2 – траектории положительногоCu+2 (Ar = 63,5 а. е. м.) и отрицательного SO4-2- (Ar = 96 а. е. м.) ионов соответственно, толстая линия между этими кривыми – траектория центра масс продиссоциировавшей молекулы.
Положение центра масс рассчитывается по определению

после численного решения уравнений (4.4) встроенным в приложение методом Рунге–Кутта (C. D. Runge – M. W. Kutta) [11, 14] для каждого иона.


Из приведённых рисунков видно, что частицы движутся по искривлённым «циклоидам» с границей на начальном радиусе. А центр масс - по весьма сложной кривой.
Если рассматривать положительный ион, то на начальной стадии всё происходит, как и предполагалось выше. Но по мере приближения к оси установки, электрическое поле может остановить ион, и ларморовская окружность не будет завершена.
Система уравнений (3.1) также имеет первый интеграл, который можно получить из закона сохранения энергии



Из первого интеграла (4.7) также видно, что положительный ион не может приблизиться к оси ближе начального радиуса, а отрицательный – не может удалиться дальше.
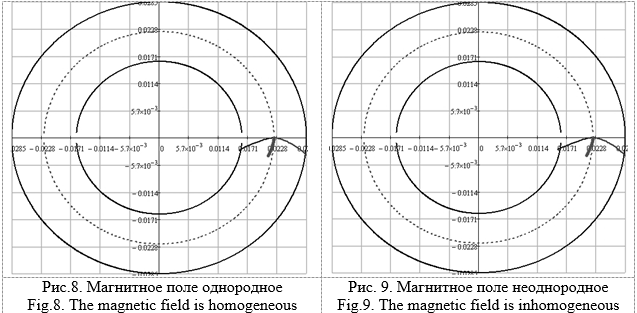
Рисунки 4 и 5 отличаются также структурой магнитного поля. На рис. 5 поле неоднородное, соответствует эксперименту, а на рис. 4 – однородное.
В случае неоднородного магнитного поля, поскольку индукция поля уменьшается при увеличении r, а положительный и отрицательный ионы движутся от средней линии rs в радиально противоположных направлениях– первый в область меньшего, а второй – большего поля, то их ларморовские радиусы будут, при прочих равных условиях (одинаковых массах и заряде), увеличиваться и уменьшаться, соответственно (см. (4.9)).
Достаточно сложное «циклоидальное» движение частиц, изображённое на рисунках 4 и 5, может быть представлено в виде совокупности двух движений – циклотронного вращения и некоторого среднего, дрейфового движения [12, 15], осуществляемого, как положительными, так и отрицательно заряженными частицами по часовой стрелке по окружности перпендикулярно скрещенным магнитному и электрическому полям. Скорость этого дрейфового движения не зависит от заряда и массы частицы и может быть оценена по формуле [10, С.32] ,
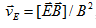
которая в нашем случае принимает вид
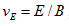
, где величины полей берутся на начальном радиусе. Сопоставление расчётов, проведённых по данной формуле, с описанными численными расчётами даёт достаточно хорошее совпадение.
Поясним теперь, почему для проведения расчётов понадобилось использовать завышенное магнитное поле. Причина этого заключается в том, что при величине поля, применяемой в эксперименте, частица выходит из исследуемой области, не совершив даже одного цикла, как это показано на рисунках 8 и 9.Завышенное же магнитное поле позволяет «удержать» ионы, получившиеся при диссоциации молекул, в области между электродами, и промоделировать их последующее дрейфовое движение. Сравнение же результатов реального эксперимента и численных расчётов, давшее достаточно хорошее согласие, показывает, что такой подход является вполне оправданным.
Заключение. Рассмотренный в данной статье пример демонстрирует возможность интеграции компьютерного моделирования в натурный эксперимент. Такой комплексный подход к организации демонстрационного эксперимента по физике в высшей школе, как показывает наша практика, является достаточно эффективным. Это подход включает в себя как подготовку непосредственно натурного эксперимента, для чего вполне можно привлекать в той или иной форме самих студентов, так и его компьютерное моделирование, а по возможности, и аналитическое описание. Всё это позволит глубже понять физику изучаемых явлений, уяснить различные тонкие моменты, поскольку для студентов педвузов, будущих учителей физики, просто пассивно «посмотреть» эксперимент и ограничиться его качественным объяснением, с нашей точки зрения, недостаточно. Что касается конкретного примера, рассмотренного в настоящей работе, то здесь нужно пояснить следующее. С целью упрощения расчёты были проведены для движения частицы в вакууме. Использование такой упрощённой модели эксперимента обусловлено её доступностью для понимания и реализации большинством студентов, обучающихся по программам педагогических вузов. Более же реальная модель эксперимента представляет собой задачу, заключающуюся в описании движения вязкой жидкости (электролита) в заданной геометрии в стационарных электрическом и магнитном полях и в наиболее общей постановке представляет собой весьма сложную задачу магнитной гидродинамики. При ряде упрощающих предположений эта задача была рассмотрена авторами в публикации «Натурный эксперимент по вращению электролита в электрическом и магнитном полях и его аналитическое описание» [3].



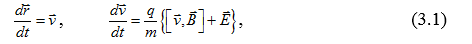
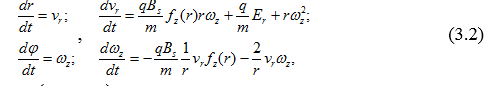
 циклотронная частота, взятая со своим знаком (её знак определяется знаком заряда частицы q),
циклотронная частота, взятая со своим знаком (её знак определяется знаком заряда частицы q), 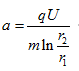 - параметр, характеризующий электрическое поле, то система уравнений (3.2) принимает вид
- параметр, характеризующий электрическое поле, то система уравнений (3.2) принимает вид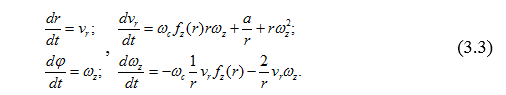







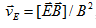 которая в нашем случае принимает вид
которая в нашем случае принимает вид 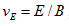 , где величины полей берутся на начальном радиусе. Сопоставление расчётов, проведённых по данной формуле, с описанными численными расчётами даёт достаточно хорошее совпадение.
, где величины полей берутся на начальном радиусе. Сопоставление расчётов, проведённых по данной формуле, с описанными численными расчётами даёт достаточно хорошее совпадение.

















Список литературы