DOI:
10.18413/2313-8971-2019-5-2-0-3
Роль математических курсов в формировании и развитии исследовательских компетенций студентов в социально-экономической сфере
Aннотация
Современные общественные тенденции положительно сказываются на деятельности исследователей, способных улучшить социальную и экономическую реальность, проанализировать изменения, наметившиеся в упомянутых областях, а также разработать более продуктивные теории и стратегии, которые позволяют людям противостоять угрозам современного мира. Следовательно, подготовка специалистов в социально-экономической сфере должна рассматриваться в качестве ключевой задачи. Крайне важно сформировать у студентов соответствующих специальностей базовые математические знания и навыки, помочь этим людям выполнять свои профессиональные функции и использовать основные источники информации, а также различные математические методы, которые могут эффективно применяться в экономике и социологии. В соответствии с результатами эксперимента, только 8,6% показали высокий уровень готовности, в то время как подавляющее большинство продемонстрировало средний (46,9%) и низкий (44,5%) уровень. Желание проводить научные исследования было выявлено лишь у 13,6% участников. Большинство респондентов (64,2%) не считают, что математика понадобится им в будущей профессии. Полученная информация свидетельствует о том, что целенаправленная деятельность обеспечивает формирование успешного образовательного пространства для будущих специалистов. Исследование включает количественный и качественный анализ сведений, полученных в рамках педагогического эксперимента. На основании данного исследования мы определили ряд образовательных факторов (аспектов), повышающих эффективность будущего специалиста. К ним относятся ментально-ценностные, организационные и ценностно-ориентированные. Люди с высоким уровнем креативности обычно рассматривают исследовательскую деятельность как фактор значительной внутренней мотивации: их умственный потенциал превышает интеллектуальные усилия, необходимые для достижения положительных результатов. Преподаватель должен учитывать и поддерживать эту мотивацию, а также желание студента предложить необычный способ решения стандартного математического задания.
Ключевые слова: математика, профессионалы в социально-экономической сфере, исследовательская готовность, педагогический эксперимент, высшее образование
К сожалению, текст статьи доступен только на Английском
Introduction. Contemporary social tendencies include strategies which “give birth” to scientists capable to ameliorate social and economic environment, explore current situation in the relative fields and propose more effective theories and methods that enable the humankind to face the challenges of the reality. Therefore, training professionals in the socio-economic field (PSEF) should be considered as an urgent issue. (Belenchuk, 2016).
The comparative analysis of scientific literature has demonstrated that modern pedagogics is most interested in the process of educating research workers in humanities. Less attention is given to the training of sociologists and IT professionals. Hence, it is crucial to elaborate the principles and generate the methods of training specialists in various areas: managers, sociologists, etc.
Based on the data obtained via using professional educational methods (Sukhodimtseva, 2017), we have singled out five additional methodological approaches for PSEF training, which are regarded as the most productive: systematic, cultural, competence-based, context-oriented and activity-focused.
A systematic approach deals with preparedness for research readiness as a complex of interwoven and interdependent elements. The strengths of this approach enable the teacher to be successful in helping different kinds of students. A cultural approach considers the influence of educational environment on representatives of different social, ethnic and other groups. It helps people to fulfill their potential, favours continuous self-development and professionalization. A competence-based approach (which E. Nikitina regards as the key one (Nikitina, 2014b)) provides students with the information they will need to write scientific articles and improves the level of their everyday professional activity. A context-oriented approach appears to be particularly significant, since it provides for better and faster acquisition of necessary skills and knowledge via designing professional environment and due to certain research methods. (Nikitina, 2016). An activity-focused approach makes analysis and modeling less labour-intensive within activity theory. In accordance with this approach, a school child or a university student is the subject of two interrelated processes: education and cooperation of pedagogues. (Korzhuyev, 2009)
These approaches underly the proposed model which aims to develop the students’ research preparedness in the system of Russian and foreign higher education in mathematics.
Research methods. Today, mathematics plays a big role in socioeconomics, being particularly important for managers, sociologists and marketing experts. Therefore, it is needed to provide students of relevant specialities with basic mathematical knowledge and skills, to help these people fulfill their professional functions and use the main data sources, along with various mathematical methods, which can be effectively implemented within sociology and economics. It should enable PSEF to understand the significance of mathematics for the formation and development of preparedness to pursue the chosen profession. (Sukhodimtseva 2016).
Natalya Prosolupova (2011) and Marina Sergeeva (2015) have rich experience in sharing their knowledge with students of humanitarian specialities, who commonly do not want to study mathematics and regard it as a supplementary or even superfluous discipline in their future profession. Such an attitude appears and develops in secondary school, which leads to poor results at the Unified State Exam and lack of motivation in the course of studying this subject within higher education.
When teaching mathematics to future linguists, psychologists and so forth, university teachers conventionally use two educational approaches. According to the first approach, the discipline is considered “general”, not directly linked to the speciality being received, and so its function is seen in the general enrichment of students’ scope and “mental image”. In conformity with the second approach, mathematics is a core subject, which, as “the mother of sciences”, is part and parcel of every academic discipline. Therefore, it should facilitate the acquisition of competences associated with this or that humanitarian field. Supporting the second approach, we would like to emphasize its compliance with interdisciplinary character of modern education that has become especially distinct over the recent decade. Numerous studies into the issue proved the need to amplify the present course with a research element characterized by using mathematical simulation, which is useful for students’ professional abilities and overall potential. Consecutive development of professional competence, gradual shift from one level of difficulty to another, is certainly the best strategy, since it conforms to the key pedagogic principles: continuity and consistency. Hence, it is crucial to include the simulation courses in mathematics in the PSEF first-year curriculum, combining formal tasks with creative assignments that develop students’ imagination, verbal skills and decision-making abilities. (Nikitina, 2014a)
Thus, mathematical simulation can be used by teachers working with future PSEF to analyze social and economic activity, which will improve the students’ research skills and make them more motivated to show better results in the educational process.
We single out the following functions of the higher mathematical education.
Educational: the models formation requires the classification of the achieved results, which considerably affects the effectiveness of mental activity (considering such basic processes as analysis, synthesis, comparison, etc.);
Self-focused: mathematical simulation transforms semi-chaotic humanitarian thinking into a solid structure (both generally and professionally);
Prognostic, i.e. predicting, working with scientific hypotheses. Future PSEF are expected to foresee the results of their study, along with potential problems and side effects, by using mathematical principles;
Motivational: the study of certain situations favours the students’ proactive education, i.e. it forms psychological skills and abilities associated with the given area;
Reflexive: mathematical simulation contributes to the analysis of one’s personal resources, to moral and cognitive justification of tasks and methods.
Research results. The detailed analysis of the articles in which the authors have examined the research constituents of students’ training (Prosolupova, 2011; Sergeeva, 2015) allows us to propose a draft definition of the notion “future PSEF research preparedness”. This phenomenon is regarded as a person-focused higher education providing for successful professional activity within the chosen speciality. It has the following aspects: motivation-based, cognitive, practical, perceptive and creative (Sukhodimtseva, 2014).
The motivation-based aspect is a complex of the student’s prevailing motives (cognitive, social, professional), which underlies his or her attitude to academic research and its structure.
The cognitive aspect, crucial for future PSEF, is associated with essential theoretical data, which enables the students to comprehend the social and heuristic significance of their professional field. This aspect may be divided into three subaspects: general, technological and domain-specific.
The practical aspect is seen as a system of research skills and abilities implemented to achieve positive results, fulfilling certain mental operations (synthesis, analysis, comparison, etc.). This aspect includes methodological, organizational and communicative competences. The first ones are the use of mathematical methods to examine social and economic factors; the qualitative and quantitative analysis of applied information; reflecting over the obtained results and making relevant conclusions. The organizational competences are represented by formulating the aim and the tasks of the scientific research, designing a detailed research plan, selecting literature and other materials. The communicative competences include: talking to a respondent in a proper manner, searching for scientific data both in printed works and on the Internet, effective use of mathematical methods in written and oral discourse.
The perceptive aspect deals with numerous perceptive skills and abilities: self-awareness, self-evaluation, assessment of external circumstances.
We interpret the creative aspect as a cluster of personal qualities most important for researchers’ effectiveness and students’ creative potential. The authors of the article have singled out the following traits which are essential for educating future PSEF: the capability to understand the problem and to dispose of it, to propose unconventional decisions, to comprehend an issue from various positions.
We have developed the criteria for future PSEF to assess their preparedness for research work, which are promotional-incentive (striving for professional success, positive emotions, predominance of internal motivation); conceptual-logical (key and additional competences, choosing solid and convincing arguments); operational (ability to implement methods characteristic of the socio-economic research, to interpret the obtained information and to present it to readers or listeners), self-rating (the ability to monitor one’s own activity, to assess an achieved competence level, to correct the research plan in accordance with circumstances, to evaluate the chosen methods), subjective-creative (the ability to identify a problem, formulate and solve it, along with readiness to focus on the key points giving enough attention to supplementary ones, to think independently and propose unconventional methods and approaches.
Based on the components of research preparedness and the enumerated criteria, the authors of the article have singled out and explained three preparedness levels: high, average and low. 81 first-year students of Kursk State University (specialities “Human resource management”, “Marketing”, “Organization management” and “Sociology”) participated in the empirical study carried out at the formation stage of our research during 2015/2016 year of study. The participants’ initial preparedness levels were determined via observation, questioning and cognitive method, along with the tasks checking the understanding of the special texts by Johnson and Mechrabian. The authors of this article have proposed generalized evaluation of the future PSEF’s general ability level within research activity.
According to the results of the experiment, only 8.6% have shown a high preparedness level, while the vast majority has demonstrated an average (46.9%) and a low (44.5%) level. The desire to fulfill scientific research has been identified in as few as 13.6% of the participants. Most respondents (64.2%) think that they will not need mathematics in their future profession. 76.1 of the students cannot answer questions formulated in original way, while only 23.9 % explain their ideas clearly and without inappropriate confusion.
The obtained information demonstrates that purpose-focused activity favours the creation of effective educational environment for future PSEF. In such conditions they will be able to develop research skills and abilities within higher mathematical education.
We have designed the model of improving future PSEF’s preparedness for research activity in the mathematical field.
The substantive stage of the experiment deals with research activity aimed to shape and develop preparedness constituents which are essential for scientific work.
The proposed preparedness model is used at three stages within three university terms.
The dialogical and collaboration-oriented principles form the didactic basis of the reproductive-algorithmic stage.
The teaching process has various aspects improving the students’ mental and communicative skills through mathematical methods. These aspects are based on dialogues, i.e. brainstorm activity, the joint analysis of problem situations and discussion of possible criteria. A particular attention was given to story problems including core mathematical concepts and to the ways of using these concepts within the chosen profession. Solving such tasks develops the students’ skills and abilities associated with analysis, comparison, distinguishing principal information from supplementary one and describing basic life situations in mathematical notions. Besides, it should be noted that professional links increase the future PSEF’s mental activity when studying mathematics, which should lead to effective independent activity outside the classroom.
The partially productive stage focuses on the difficulties with didactic materials. Three years ago, we began our course with special lectures, which included heuristic situations and traditional lectures followed by “mini-workshops” (short discussions). The emphasis was put on dynamic professional tasks requiring certain skills and abilities of research character, such as monitoring, comparing and hypothesizing. Such tasks are team-oriented and create relevant conditions for the student-focused approach relying on mathematical simulation within the student’s individual activity. The authors have designed a supplementary course “Mathematics in Humanities”, aimed at making students acquainted with mathematical operations and techniques used in socioeconomics. We have elaborated peculiar tasks and theoretical fragments with a creative component that are not integrated into the basic programme. The level of PSEF’s motivation has significantly increased, which enabled us to organize extra-curricular activities (workshops, research projects, students’ scientific clubs, etc.).
The experience-based and creative stages presuppose the prevalence of the creative component over reproductive and productive ones. Within this stage, the students participate in generating original scientific topics and various situations requiring an uncommon approach. The lectures include some intentional mistakes, heuristic assignments and dynamic tasks for self-controlled learning (both for groups and certain individuals). The scientific activity beyond the given curriculum has had several creative vectors. The participants were involved in the improvement of educational practice in mathematics, conducted autonomous research within voluntary groups and presented their results at the scientific conference “Mathematics and its implementation in modern theoretical and applied areas”.
The graph given below demonstrates the difference between the initial and post-experimental data (Fig. 1)
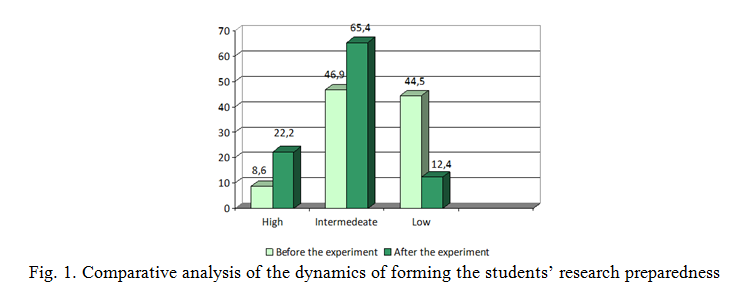
We can see a noticeable progress in the levels of research preparedness: the number of low-level participants has decreased by 3.1%. At the final stage of the experiment, most future PSEF (65.4%) confirmed their average preparedness level. These alterations have been studied based on T-criterion by Frank Wilcoxon. In accordance with the results of the conducted experiment, there is evident positive dynamics in the students’ preparedness for research activity (the level of confidence is 0.95).
This improvement is due to some theoretical fragments integrated into the educational programme and to its conformity with the pedagogical essence of the experiment.
Besides, through c2 criterion the authors of the article visualized a rather significant difference in the distribution of the research preparedness constituents before and after the experiment. Negligible discrepancy between predicted and achieved results allows us to regard them as a natural effect of innovative training methods used with first-year students.
Thus, the data correlation of the summative vs formative results has proven this model and educational environment to be effective tools in training students’ research readiness.
Discussion. Based on the quantity-quality data analysis made during an educational experiment, we have found out some learning modalities, which intensify the efficiency of future PSEF’s research preparedness; axiological, organizational and reflexive-axiological issues.
1. Axiological issue
– The development of value perception of scientific-research work through exploring and mastering mathematical models of social phenomenon.
Mathematical modeling allows the students to carry out research in the theoretical area within their trades, to learn periodic and special literature, to pursue a creative search. The development of scientific-research awareness is a long, multi-aspect and difficult process, with stable results through experience. Most Professors of Practice believe that the limits of scientific research work in higher education are within writing course and diploma papers. From our point of view, this is a unilateral approach of training specialists. The efficiency of researchers’ awareness will increase if different relevant tasks with gradually added complication are included into the curricular for first-year students. In particular, mastering the course of higher mathematics involves employment of certain research-based and imitational tasks, which provide the description of different mathematical models in the context of future occupation. Educational process should drive students to understand the importance of methods in their pursuit to be a responsive creative-oriented specialist, who is highly demanded in modern society.
– The creation of positive psychological atmosphere based on mutual respect and common creative activity in carrying out research and simulation-research tasks.
The subject of research is to be challenging and enjoyable. Success in work depends on the evidence of emotions involved. Recipathy and mutual respect are the most important factors in educational context. The teacher nowadays is to be skillful not only in interpreting scientific information but also in arranging advisees’ self-instructional work aimed at developing their skills and competence.
– The creation of a close collaboration and mutual support atmosphere through involvement of students in common activity in class-rooms, as well as in self-instructional work.
PSEF are often involved in spitball analysis. The logicality of intellectual operation evolution is a triple-transcendence operation: from content to apprehension, then from apprehension to argumentation and, finally, from argumentation to function. Therefore, collective mental activity is reasonable enough in studying mathematics as it helps students to scrutinize variety of options, to argue for their positions, to cogitate at individual and group levels (i.e. to configure-to-levels, to state the compliance extent of the data gained to the aims of the research, to get the idea of their responsibility for team’s failure).
2. Organizational issues.
Gradual complication of the simulated research elements based on the mathematical models of the SEA phenomena, which prepare for the switch from traditional (reproductive) to innovative (problem-heuristic) way in didactic data handling.
Mathematical simulation offers challenging methods for future PSEF’s contemplation. The congruent methods and the models enclosed can be treated as a universal tool and they also pursue the outcomes at an advanced level of formalization and characteristic generalization of the most important connections in studying economic phenomena and procedures. As a result, teaching the student to apply mathematical simulation in social process analysis helps to prepare a better-trained specialist. The implementation of this approach in higher education has some advantages: it provides didactic component integration into different professional domains; it fosters positive motivation in research; develops independence and autocriticism; empowers students’ creative potential. The professional-research situations should be gradually included into the curriculum, with every succeeding model containing situations that are more complicated. In terms of an individual vector of scientific-research preparedness formation, one should move from practical dimension in reviewing mathematical concepts to independent task execution. The teacher is supposed to correlate the complexity level of text tasks and their control to individual students’ aptitudes. The process is to be of a didactic nature aimed at common creative work and realized in two main formats ‘teacher – student’ and ‘student – student’
According to A. Verbitsky, a dialogue rendering method intensifies the problematicity level and, as a result, stimulates the outcomes of education (Verbitsky 1960; Verbitsky 2004). Though problematicity is an indicative value of research work, we have found it feasible to study problem situations in both groups and the whole team. These tutorial methods promote research-thinking development, an ability to communicate and intensify a wide range of mental activity.
– The creation of interdisciplinary research environment combined with research work inside and outside class-rooms.
In the context of higher education, it is very important to form a team, whose members share the same ideas, who are specialists in the same field and enjoy personal and professional communication within this team. The teacher should bolster students’ concern with research work during the term-time and during Off-Campus Employment to bring about some social-approval products (participation in conferences, material publishing and work at a project). A person who studies at educational institution (probably externally) must have a chance to estimate his or her merits in research, to reveal his or her creative potential and self-confidence in occupational ability. Therefore, it is quite reasonable to create an interdisciplinary work-related research environment at academic institutions and integrate research both during the classes and at extracurricular time.
– Outlook actualization within the depth and extent of aspects of mathematical knowledge in terms of practical work-related components.
The origin and development of research activities are stipulated by the need of an individual to get new information, to enhance obtained knowledge in definite subjects, to explore methods that are more effective in work. If through the teacher’s appropriate endorsement a student realizes the way to define a forthcoming problem preceded by the analyses of tasks given by the teacher, the student’s research readiness level will rise. The teacher is not believed to “spoon-feed” the material, but to deliver it in a rigorous thoughtful fashion to promote students to the advanced level.
– Development and readiness level consideration, realization of complementary approaches – both individual and differential.
As most students at economic and sociological departments are interested in humanitarian subjects, it is reasonable to address their educational foundation and use a con-centrum principle in-group work (i.e. material is assigned in relatively closed loop cycles).
3. Reflexive-axiological issues
– Image creation “I am a researcher” for future PSEF.
In the course of the study the authors of this paper encouraged the students to evaluate their individual traits, their evolution habitude and adequacy in work-result precognition, as well as their constant preprofessional self-realization in terms of their scientific readiness. Positive “I-concept” formation and its intensification perk up their confidence, nourish their ability to realize their real and ideal “I-image”, treat adequately their current positions and prospects for future development.
– Development and enhancement of reflexive-research notions through research tasks realization, analysis of the available results as well as through the process of regulation and control of research behavior patterns.
A clearly articulated reflexive-research stand helps an individual communicate effectively with different groups of people, adapt to a particular purpose or a changing situation. A dialogue form is the most productive way to develop reflexive reasoning. It is very important to be able to check and control the process of work, to predict results, to adjust the strategy to research behavior patterns, to realize motivation of other people and identify their principles in speculation. The negative-experience (errors and inaccuracy) analysis should be included in the educational process, as this kind of activity is helpful in work apprehension and critical thinking. Moreover, the teacher is to inspire students for in-depth reflection, and avoid any formality in training no matter it concerns the students or the teacher. Internal discourse is the most advanced level. It can be gained on a parity-based discussion between a teacher and advisees, the latter being active and encouraging students to be active as well.
– Monitoring the level of students’ intellectual commitment, research creativity in different fields in terms of the work done.
Conclusion. Formation of research preparedness in mathematical disciplines presupposes students’ work with story problems, including mathematical characteristics of socio-economic phenomena, scientific tasks, assignments with interrelated questions and heuristic approach-dependent tasks. It should be noted that the assessment criterion should not be used for any types of activity oriented to reveal the students’ creative potential. For example, a test should be a free-response one and has to concentrate on checking practical knowledge and relevant skills. As a rule, highly creative people regard research activity as a source of intense internal motivation: their intellectual energy prevails over mental efforts needed to fulfill the assignment. Such an initiative must be noticed and supported by the teacher, along with the wish to propose an original solution of a conventional mathematical task. Story problems should not be approached stereotypically, through a standard algorithm. They should be used by the pedagogue to reveal his/her students’ imagination and creative potential.
Список литературы
Список использованной литературы появится позже.