Введение. Федеральные государственные образовательные стандарты высшего образования предъявляют новые требования к качеству профессиональной подготовки педагогических кадров. Эти требования связаны, прежде всего, с компетентностным подходом к результатам и целям обучения, что влечет за собой изменение программ учебных дисциплин, учебников, методического обеспечения и т.д. В свою очередь, повышаются требования работодателей к уровню подготовки будущих педагогов. Современный педагог должен уметь продуктивно работать в условиях уровневой и профильной дифференциации, вариативности программ и учебников, освоения и внедрения в учебный процесс новых информационных технологий, создавать новые электронные ресурсы, применять методы математического моделирования и статистики. Это указывает на необходимость формирования у студентов педагогических направлений профессиональных компетенций, включающих совокупность профессиональных знаний, умений и навыков, способность их применения для решения ситуационных задач, которые ориентированы на самостоятельное участие личности в учебном процессе.

В наступившую эпоху математизации наук особенно актуальной становится проблема повышения уровня математической подготовки студентов-бакалавров педагогических направлений. Однако в настоящее время можно говорить о недостаточном развитии математического мышления выпускников педагогических вузов, о неумении применять методы математического моделирования с использованием компьютера, использовать идеи и методы математики в интеграции обучения дисциплинам математического, естественнонаучного и гуманитарного направлений.

Это приводит к необходимости организации научных исследований, направленных на поиск и проектирование методических подходов к обучению математическим дисциплинам студентов-бакалавров педагогических направлений, актуализирующих межпредметные связи математики через внедрение интегрированных программ, модульного обучения, электронно-информационной образовательной среды (ЭИОС) и метода проектов и способствующих формированию профессиональных компетенций обучающихся.

Вопросы подготовки компетентного конкурентоспособного специалиста отражены в работах В.И. Байденко, А.В. Баранникова, А.Г. Бермуса, В.А. Болотова,
Э.Ф. Зеера, М.В. Рыжакова, В.В. Серикова, А.В. Хуторского, В.Д. Шадрикова и др.

Идеи организации педагогического процесса с позиции интегративного и компетентностного подходов представлены в работах М.Л. Вайнштейна, Е.В. Ткачено, Н.К. Чапаева, А.К. Шелепова, Н.О. Вербицкой, Э.Ф. Зеера, H.A. Зимней, Д.И. Котовой, Г.М. Романцева, В.А. Федорова,
A.B. Хуторского и др.

Проблемой совершенствования математической подготовки студентов педагогических вузов занимались С.Г. Григорьев,
В.А. Гусев, В.А. Далингер, С.Д. Каракозов, М.П. Лапчик, В.Л. Матросов,
В.М. Монахов, Н.И. Рыжова, Г.И. Саранцев, И.М. Смирнова и др.

Вопросы проектирования учебного процесса с применением инструментов и сервисов электронного обучения рассматриваются в зарубежных и отечественных публикациях: применение онлайн технологий (Ализарчик, Голяс, 2016; Boloudakis, Retalis, 2018; Didenko, Aksenova, Loginova, 2016; Ellis, Bluc, 2016 и др.), медиа-визуальных коммуникаций (Yarkova, Cherkasova, 2017 и др.), дистанционного обучения в сетевой среде (Zhai, 2018 и др.) и т.д.

В нашей работе сделан акцент на анализе современных исследований проблемы обучения математическим дисциплинам в системе высшего образования на основе интегративного подхода. 

Перминов Е.А. исследует содержательное направление интеграции на примере «Дискретная математика». Автор решает проблему разработки методологических, математических, психологических и дидактических аспектов реализации межпредметных связей на основе дискретной математики в математической, естественнонаучной и профессиональной подготовке будущих учителей математики, информатики и инженеров-педагогов в условиях перехода на компетентностную модель образования. Таким образом, ядром содержательного направления интеграции образования является идея реализации межпредметных связей (Перминов, 2013).

Ряд авторов предлагает использовать потенциал междисциплинарной интеграции, реализуемой при условии внедрения в учебный процесс информационных и образовательных интернет-технологий (Бушмелева, 2017; Ализарчик, Голяс, 2016 и др.)

Симонова И.Э., Сагателова Л.С. рассматривают интеграцию содержания математического образования в контексте повышения его качества в техническом вузе. Следуя авторской концепции, в курс математики должны быть внесены следующие принципиальные изменения: создание технологий двуязычного преподавания математики как интегративной модели научной и практической деятельности; создание интегративных курсов математики и естественнонаучных дисциплин, математики и общественных наук; осуществление обучения и диагностики математических знаний с учетом прикладной и профессионально-ориентированной направленности содержания обучения; формирование и развитие у студентов умения строить математические модели явлений окружающего мира (Симонова, Сагателова, 2014).

В исследовании Радионова М.А., Федосеева В.М., Шабанова Г.И., Акимовой И.В. рассмотрены особенности проектирования технологического компонента методической системы обучения математике бакалавров, организованной на принципах интеграции их математической и инженерной подготовки (Родионов, Федосеев, Дедовец, Шабанов, Акимова, 2018).

В работе Попова Н.И., Никифоровой Е.Н. исследованы методические подходы при экспериментальном обучении математике студентов вуза, предполагающие комплексное использование в учебном процессе электронного курса, компьютерных тестов, учебных пособий и ключевых математических задач (Попов, Никифорова, 2018).

В статье Н.А. Прокопенко представлено оригинальное дидактическое средство обучения математике студентов технического университета – интегрированное учебное пособие. В концепции автора, интегрированное учебное пособие – это пособие, реализующее интегративный подход к обучению, основанный на принципах научности, целостности, непрерывности, объективности, индивидуализации и дифференциации обучения. Главной особенностью такого пособия является возможность его использования в обучении как математике, так и других дисциплин, в которых применяется математический аппарат для решения задач (Прокопенко, 2017).

Таким образом, содержательное направление интеграции позволяет актуализировать межпредметные и внутрипредметные связи через внедрение различного рода интегрированных программ, интегрированных курсов, модульного обучения, метода проектов, электронно-информационной образовательной среды (Аганина, Телекбаева, 2012; Ализарчик, Голяс, 2016; Бушмелева, 2017; Родионов, Федосеев, Дедовец, Шабанов, Акимова, 2018; Попов, Никифорова, 2018; Федосеев, 2016; Salyakhova, Valeeva, 2015; Dragana, Dragan, Stojan, 2018); наиболее полно проблема обучения математическим дисциплинам в аспекте содержательной интеграции образования рассмотрена для студентов технических вузов; для студентов-бакалавров педагогических направлений указанная проблема рассматривается для конкретных профилей на примере конкретных дисциплин.

Основная часть. Целью статьи является представление опыта, анализ и обобщение результатов внедрения частных методик на основе компетентностного и интегративного подходов при обучении математическим дисциплинам студентов разных профилей педагогического направления в системе бакалавриата.

Методология исследования опирается на обобщение зарубежного и отечественного опыта обучения студентов в вузах.

В процессе экспериментальной работы используются методы эмпирического исследования: наблюдение, педагогический эксперимент, проведение педагогических измерений, экспериментальное обучение математическим дисциплинам («Численные методы», «Геометрия», «Исследование операций», «Основы математической обработки информации»); методы теоретического исследования: анализ научно-педагоги­ческой, психологической, философской литературы и диссертационных исследований, теоретический анализ методической и математической литературы по проблеме исследования, анализ вузовских программ, учебников и учебных пособий по математическим дисциплинам, анализ организации процесса преподавания математических дисциплин для студентов-бакалавров педагогических направлений.

Результаты. Выбранный нами компетентностный, интегративный подходы предполагают такую организацию процесса обучения математическим дисциплинам, которая позволила бы студентам эффективно усваивать учебный материал, учитывая межпредметные связи математики и способствуя формированию профессиональных компетенций. Это приводит к необходимости проектирования и внедрения в учебный процесс электронных курсов, информационных образовательных ресурсов, интегративных и компетентностно-ориентиро­ванных заданий, интеграцию образовательных технологий, применение методов психологической, педагогической, социологической диагностики в единстве с методами математической статистики.

В связи с этим для обучения студентов-бакалавров педагогических направлений математическим дисциплинам были спроектированы электронные курсы «Численные методы», «Геометрия», «Исследование операций», «Основы математической обработки информации» на базе платформы Learning Management System Moodle, с применением инструментов и сервисов электронного обучения. Для организации самостоятельной работы и проведения практических занятий были разработаны учебные пособия, реализующие концепцию содержательной интеграции образования с актуализацией межпредметных связей (численные методы – информатика; геометрия – информатика и современные средства оценивания результатов обучения; исследование операций – информатика; основы математической обработки информации – информатика и дисциплины, определяемые профилем направления: биология, география, литература, иностранный язык и т.д.).

Так, в 2017-2018 учебном году процесс обучения студентов педагогического направления профилей «Математика и Информатика», «Информатика и Физика», «Информатика и Английский язык» осуществлялся с использованием электронного курса «Численные методы». Курс включал в себя следующие модули:

– краткий конспект лекций (структурированный теоретический материал);

– образцы решений типовых задач;

– задачи для самостоятельного решения (с ответами);

– вопросы и задания для самоконтроля;

– итоговая аттестация в форме тестирования.

В процессе организации самостоятельной работы студентов использовалось учебное пособие “Численные методы”, в котором представлены: модульно-рейтинговая система обучения студентов; индивидуальные задания по модулям дисциплины и методические рекомендации к их выполнению; задания, связанные с представлением вычислительных алгоритмов в среде Pascal ABC и актуализирующие знания в области использования языков и методов программирования (Фомина, Буяковская, Долматова, 2018). В ходе анкетирования с целью выявления эффективности указанного пособия, обучающиеся отметили возможность оптимизации времени на подготовку к практическим занятиям и лабораторным работам, более глубокое осмысление теоретического материала, совершенствование навыков решения практических задач с применением языков программирования.

Таким образом, в ходе педагогического эксперимента в 2017-2018 учебном году в курсе дисциплины «Численные методы» осуществлялось комплексное использование авторского учебного пособия, электронного курса, интегративных заданий, а также технологий группового обучения (Экспериментальные группы МИ-13, ФИ-13, ИА-13). В контрольных академических группах МИ-12, ФИ-12, ИА-12 указанные методические подходы не использовались. Всего в эксперименте было задействовано 80 респондентов.

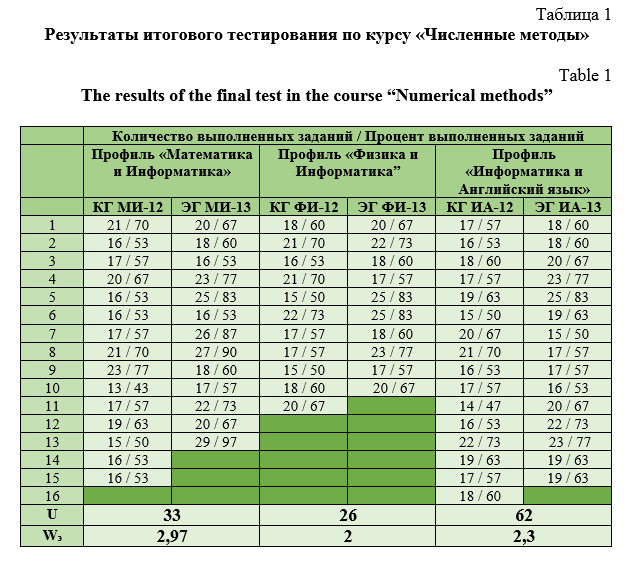
Для проведения аттестации знаний по курсу «Численные методы» был использован итоговой тест, содержащий 30 заданий. Результаты тестирования с указанием академических групп представлены в табл. 1.

Распределение испытуемых по проценту выполненных заданий и анализ результатов в пятибалльной системе в контрольных и экспериментальных группах представлены в табл. 2 и на рис. 1.

Для проверки гипотезы об эффективности используемых методических подходов был выбран критерий Вилкоксона-Манна-Уитни:

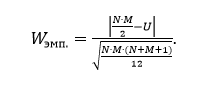
Этот критерий применяется для определения достоверности совпадений и различий для экспериментальных данных, измеренных в шкале отношений (в нашем случае − число правильно решенных задач) и позволяет проверить гипотезу о том, что две выборки совпадают по статистическим показателям; оперирует не с абсолютными значениями элементов двух выборок, а с результатами их парных сравнений (Новиков, 2010).

Проиллюстрируем статистические вычисления на примере групп профиля «Математика и Информатика» (КГ МИ-12, ЭГ МИ-13).

Для каждого элемента выборки ЭГ МИ-13 определяем число а_i элементов второй выборки, которые превосходят его по своему значению:

принимается гипотеза  достоверность различий сравниваемых выборок составляет 95%, следовательно, можно утверждать о целесообразности применения разработанной методики при обучении численным методам.

Заметим, что до начала эксперимента была проверена гипотеза  о совпадении характеристик контрольной и экспериментальной групп, которая была принята на уровне значимости 0,05 и подтвердила правомерность дальнейшего сравнения
выборок.

В основную образовательную программу бакалавров педагогического направления профиля «Математика и Информатика» включена учебная дисциплина «Геометрия». В преподавании дисциплины используется интегративный подход, реализующий межпредметные связи геометрии и информатики, интеграцию традиционных, активных и интерактивных образовательных технологий (кейсовые технологии, проектные технологии, информационно-коммуника­ционные технологии), а также метод соционического типирования для формирования эффективной проектной команды (Гуленко, 2009). Для организации самостоятельной и проектной деятельности студентов было разработано учебное пособие по геометрии, включающее в себя сведения о модульно-рейтинговой системе обучения, теорию и образцы решения типовых задач с применением графических редакторов и программ интерактивной геометрии (LibreOffice Draw, Kig, GeoGebra, «Живая геометрия» (русская версия американской программы Geometer's SketchPad), TINKERCAD), варианты контрольных работ с образцами решения, систему кейс-заданий с методическими указаниями к их выполнению, где раскрываются: особенности кейс-метода, этапы, план-график, образцы выполнения кейс-задания в стиле «Презентация», критерии оценивания работы (Позднякова, Буяковская, 2019).

Апробация и анализ результатов указанных методических подходов к преподаванию геометрии были проведены в группе МИ-16 (20 респондентов) в 2017-2018 учебном году с использованием методов анкетирования и математической статистики и представлены в работе (Позднякова, Долматова, 2018). Методом случайного отбора были сформированы две группы студентов по 10 человек в каждой: контрольная группа (КГ МИ-16) и экспериментальная группа (ЭГ МИ-16). В 2018 – 2019 годах средствами дисциплины «Методика обучения математике» была выявлена взаимосвязь уровня сформированности профессиональных компетенций студентов – будущих учителей математики и реализуемых методических подход в обучении геометрии. Так, на практических занятиях по дисциплине «Методика обучения математике» студентам было предложено профессионально ориентированное задание по проектированию технологической карты урока (ТКУ), тема которого была связана с проблемой, представленной в кейс-заданиях по геометрии. В соответствии с разработанными критериями оценивания технологической карты урока, были получены следующие результаты: «отлично» – 5 (25% от общего числа студентов), из них 4 студена из экспериментальной группы (80% от числа студентов, получивших оценку «отлично»); «хорошо» – 9 (45% от общего числа студентов), из них 6 студентов из экспериментальной группы (66,7% от числа студентов, получивших оценку «хорошо»); «удовлетворительно» – 6 (30% от общего числа студентов), из них один студент из экспериментальной группы (16,7% от числа студентов, получивших оценку «удовлетворительно»).

Для определения уровня связи и ее статистической значимости между эффективностью решения контекстной задачи (проектирование урока) и внедрением инновационных подходов к преподаванию курса геометрии (метод проектов, технология кейсов, групповые технологии, компьютерные технологии, методы социально-психологической диагностики) мы перешли к дихотомической шкале и воспользовались φ-коэффициентом корреляции Пирсона и четырехполосной таблицей сопряженности (таблица 3).

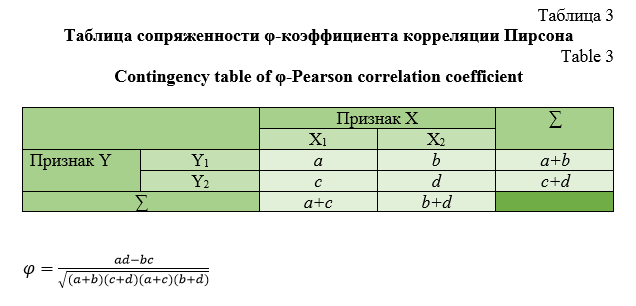
Результаты эксперимента представлены в таблице 4.

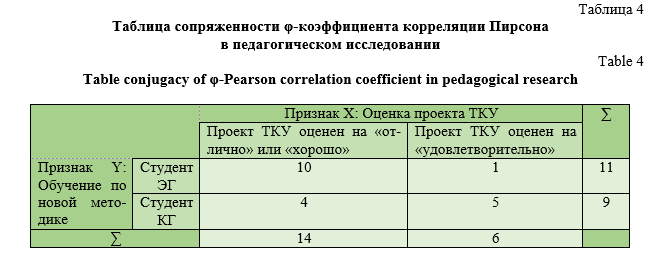
Так как коэффициент корреляции положителен, то признак «Проект ТКУ оценен на «отлично» или «хорошо»» коррелирует с признаком «Испытуемый – студент экспериментальной группы». По таблице критических значений дихотомического коэффициента корреляции находим, что коэффициент является статистически значимым для первого уровня (φ_кр.=0,44). Таким образом, можно сделать вывод, что корреляция между эффективностью решения профессионально ориентированной задачи и использованием разработанных методических подходов при обучении геометрии является статистически значимой, что можно констатировать с вероятностью 0,95.

Заключение. Подводя итоги сказанному, можно заключить, что проектирование процесса обучения математическим дисциплинам студентов-бакалавров педагогических направлений целесообразно осуществлять на основе компетентностного и интегративного подходов. Формирование профессиональной компетентности студентов осуществляется средствами учебного содержания математических курсов с применением ИКТ, электронно-информацион­ной образовательной среды и специально разработанного методического обеспечения. Внедрение метода проектов в систему обучения возможно через систему кейс-заданий с применением психолого-социологических диагностик для обеспечения эффективной групповой командной работы. Анализ и оценка результативности методических подходов проведены с помощью математико-статистических методов и подтверждают их эффективность. Это определяет перспективность дальнейших исследований в области проектирования методической системы математической подготовки бакалавров педагогических направлений на основе интегративного подхода.