Введение (Introduction). Современный многомерно-трансформирующийся мир ставит человека перед вызовами новой реальности, связанными с изменяющимися условиями общественной, политической, семейной жизни и профессиональной деятельности. Таким образом, особую значимость приобретает наличие некого культурного универсала, базирующегося на сформированности социально-психологических, так называемых “мягких навыков” или “soft skills”. Человек, обладающий такими навыками, способен принимать решения, действовать и решать повседневные и профессиональные задачи, учиться самостоятельно, прогнозировать свое развитие и оставаться конкурентным в профессиональной и индивидуальной сферах.
На Всемирном экономическом форуме в 2018 году были определены десять ведущих “soft skills” как комплекс неспециализированных, важных для карьеры надпрофессиональных навыков, которые отвечают за успешное участие в рабочем процессе, высокую производительность и являются сквозными, то есть не связаны с конкретной предметной областью. Обобщением так называемой Давосской десятки является «Система 4К», имеющая за рубежом название “Four Cs” (Collaboration, Communication, Creativity, Critical thinking)[1].
В настоящее время в системе основного образования происходят трансформации, связанные с установлением образовательных ориентиров на личностное развитие обучающегося. Эмоциональный интеллект, социальные умения и навыки (“soft skills”) являются решающим фактором личной успешности и дальнейшей социальной и профессиональной самореализации. Закономерно, что в теории и практике школьного обучения идет непрерывный творческий поиск эффективных путей решения проблемы “soft skills”. Предметами исследования становятся:
диагностика и оценка «мягких» навыков[2];
использование различных технологий, методов и приемов формирования таких навыков как на уроках, так и во внеурочной деятельности (Восторгова, Михайлов, Сыщенко, 2019);
сравнение эффективности используемых методов и приемов (Бакурова, Пузанова, 2019);
выявление особенностей развития отдельных навыков, например, критического мышления (Chou, Wu, Tsai, 2019; Sari, Sumarmi, Astina, Utomo, Ridhwan, 2021), креативности (Утемов, 2012; Kusumaningtyas, Supaman, 2020; Yaniawati, Kariadinata, Sari, Pramiarsih, Mariani, 2020; Segundo Marcos, Daza Gonzalez, Lopez Ferandez, Phillips-Silver, 2020), коммуникативных навыков (Булыгина, 2013) и т.д.
Математика, являясь инструментом системного познания мира и критического анализа объективной реальности, играет в образовании особо важную роль, а ее потенциал как школьной дисциплины может быть использован для формирования и оценки таких “мягких” навыков как:
критическое мышление (способность задавать конструктивные вопросы, анализировать, аргументировать и оценивать идеи и решения);
креативность (способность генерировать идеи и решения);
коммуникация, координация и кооперация (способность выражать и интерпретировать мысли и чувства в устной и письменной форме; эффективно взаимодействовать с другими людьми и работать в команде);
эмпатия, эмоциональный интеллект (способность понимать свои эмоции и осознавать их причины; распознавать и разделять эмоции другого человека; управлять своими эмоциями).
Цель статьи: проектирование модели формирования и оценки “soft skills” на основе открытых практико-ориентированных задач и представление опыта ее внедрения при обучении математике.
Теоретическая основа (The theoretical basis). В исследовании М.А. Пинской и А.М. Михайловой представлены модели учебных заданий по математике и естественно-научным предметам, которые открывают для учеников возможность применять и развивать компетенции «4K». Такие задания обладают следующими особенностями: учебная задача предполагает несколько решений; в центре задачи находится либо мини-проект, либо конструирование некоторого продукта с использованием нестандартных средств; задание дает возможность для развития кратко очерченного сюжета в рамках заданной проблемной ситуации; задание предполагает работу в группе с возможным выделением подзадач для автономной или парной работы; задача требует самостоятельного поиска необходимой информации (Пинская, Михайлова, 2019). Рассмотрев предложенную модель учебных заданий, можно сделать вывод, что технология формирования “soft skills” при обучении математике может быть выстроена на основе принципа приоритета открытых практико-ориентированных задач.
В исследовании М.В. Егуповой практико-ориентированная задача связана с практическими приложениями математики, представляет собой содержательную модель реального объекта, математическая модель которого может быть построена средствами школьного курса математики. Автор выделяет следующие особенности таких задач: условие задачи соотносится с содержанием школьных дисциплин (математических и нематематических) и жизненным опытом учащихся; учебный характер задачи выражен в ее соответствии известным дидактическим целям, поставленным перед школьными математическими задачами; задача является сюжетной (текстовой) задачей (Егупова, 2014).
Гин А.А., Утемов В.В. и др. выделяют открытые и закрытые учебные задачи (Гин, 2014; Утемов, 2012). Закрытая задача – это классическая учебная задача, в которой обязательно оговаривается, что дано и что не известно. Ставится четкий вопрос о том, что требуется найти. Действия и решения производятся в соответствии с алгоритмом, освоенном на уроке, и имеется, чаще всего, единственный ответ. Открытая задача может обладать следующими характеристиками: 1) отсутствует конкретное условие, четко сформулированный вопрос, известный алгоритм решения, единственно правильное решение; 2) присутствует противоречие, которое еще больше «мешает» решить задачу.
Таким образом, в открытых задачах данная или конечная цель явно не заданы, учащимся дается свобода в постановке вопроса своего исследования, в выборе метода рассуждений, во введении дополнительных параметров, необходимых для решения.
В статье N.A. Nohda проводится классификация открытых задач. Так, в зависимости от исходных данных, смыслового содержания задачи, поставленного вопроса и времени ее решения, автор выделяет задачи-исследования, жизненные задачи, задачи без явного вопроса, вариативные задачи, проекты (Nohda, 2000).
Вопросам использования открытых задач в процессе обучения математике посвящены исследования Горева П.М., Карпушиной Н.М., Овсянниковой И.С., Поздняковой Е.В., Филенко С.А., и др. Все эти авторы указывают на высокий потенциал открытых задач в области развития креативного и дивергентного мышления, исследовательских умений, универсальных учебных действий, овладения методами творческой деятельности (Горев, Рычкова, 2015; Карпушина, 2004; Овсянникова, 2014; Позднякова, 2004; Филенко, 2020).
Одним из приемов преобразования закрытой задачи в открытую является варьирование ее условия. Так, если вместо абстрактных математических объектов ввести в условие задачи некоторые реальные объекты, то это позволит не говорить обо всех требованиях, которым должен удовлетворять искомый объект. Существуют приемы наполнения отвлеченного условия математической задачи практическим содержанием, которое поможет учителю вызвать у обучающихся потребность в творческом поиске, поставить перед необходимостью искать рациональный способ решения. Сущность этих приемов состоит в подборе таких реальных объектов, замена которыми отвлеченных математических объектов позволит явно не сообщать хотя бы одно из требований, предъявляемых к искомому объекту: это требование должно явиться следствием рационального выбора условий для достижения поставленной практической цели.
Поиск рационального условия организуется методами творческой деятельности – мозгового штурма или синектики (личной эмпатии). В теории эвристического обучения мозговой штурм определяется как метод группового обучения и стимулирования познавательной активности, основанный на процессе совместного разрешения поставленных в ходе организационной дискуссии проблем. В ходе ее участников побуждают к свободному выдвижению идей с последующим их критическим рассмотрением. Синектика – это метод решения творческих задач путем поиска аналогий, частным случаем которого является личная эмпатия, когда решающий задачу представляет себя в образе системы, в которой возникла проблема (Ilevbare, Probert, Phaal, 2013).
Таким образом, мы выделяем следующие особенности открытых практико-ориентированных задач:
постановка задания вне математики, в реальной действительности, и возможность ее решения математическими средствами;
отсутствие рационального условия для достижения практической цели и его поиск методами творческой деятельности (метод личной эмпатии, метод мозгового штурма, метод дискуссии);
использование в решении метода математического моделирования;
использование метода групповой работы и метода рефлексии.
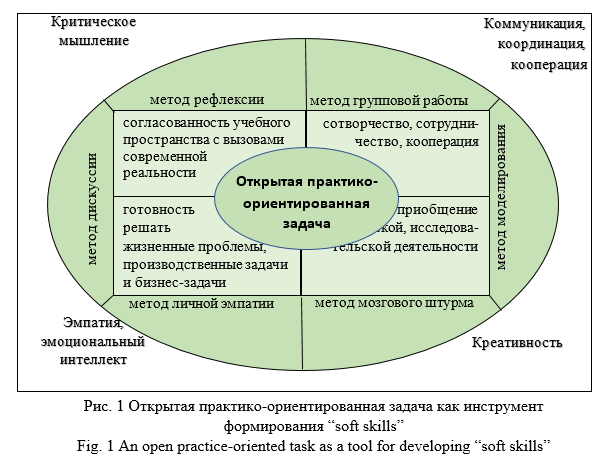
Открытая практико-ориентированная задача позволит учителю работать в нескольких направлениях:
согласованность учебного пространства с вызовами современной реальности;
сотворчество, сотрудничество, кооперация;
приобщение к творческой, исследовательской деятельности;
готовность решать жизненные проблемы, производственные задачи и бизнес-задачи (рис. 1).
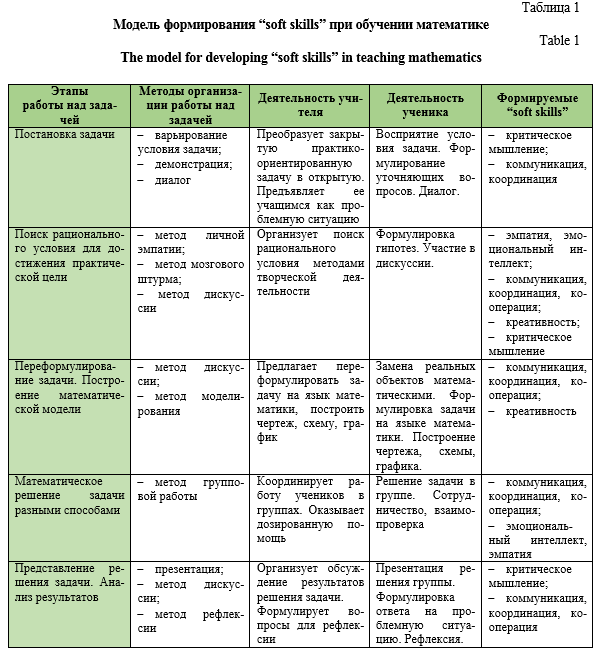
Таким образом, на основе открытых практико-ориентированных задач проектируется модель формирования “soft skills” при обучении математике. Модель детализирует деятельность ученика и учителя на каждом этапе работы над задачей, конкретизируя методы и формы работы, а также структуру и содержание формируемых «мягких навыков» (табл. 1).
Материалы и методы исследования (Methodologyandmethods). Для проверки эффективности модели формирования «мягких навыков» на основе практико-ориентированных открытых задач при обучении математике проводился пилотный педагогический эксперимент. В экспериментальную группу были включены ученики девятого класса в количестве двадцати человек.
Например, по теме «Функции и их свойства», ученикам предлагалась следующая задача: «Представьте, что вы – менеджер компании, которая занимается продажей персональных компьютеров. Ваша компания заказывает компьютеры у поставщика и доставляет их на склад, откуда их затем отправляют покупателям. В течение года ваша компания заказала 2400 компьютеров, которые могут быть доставлены на склад либо все сразу, либо несколькими партиями. Раскупаются компьютеры в течение года равномерно, т.е. в среднем 200 штук в месяц. Доставка одной партии на склад (независимо – крупной или мелкой) обходится компании в 1000 рублей. Хранение на складе одного компьютера обходится в 30 рублей. Решите, какими партиями нужно заказывать компьютеры».
Заметим, что метод личной эмпатии присутствует в самой формулировке задачи, когда ученикам предлагается представить себя менеджерами компании, занимающейся продажей компьютеров. С помощью мозгового штурма находят рациональное условие: доставка и хранение компьютеров в течение года должны обходиться компании как можно дешевле. Математической моделью заданной ситуации является функция затрат
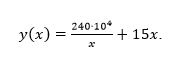
Необходимо определить, при каком значении х функция принимает наименьшее значение, где х – количество компьютеров в каждой партии.
Рассмотрим пример фрагмента урока – практикума по теме «Площадь».
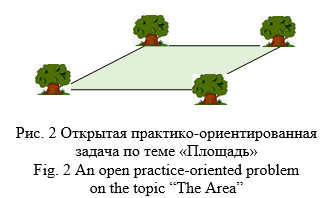
Учащимся предлагается открытая практико-ориентированная задача как проблемная ситуация (рис. 2).
В городском парке поверхность искусственного пруда имеет форму квадрата. В вершинах квадрата на берегу пруда растут четыре вековых уникальных дуба. Согласно проекту благоустройства парка, площадь поверхности пруда необходимо увеличить в два раза, но так, чтобы новый пруд сохранил форму квадрата. Как это сделать?
Поиск рационального условия организуется методом личной эмпатии. Учитель предлагает ученикам представить себя в образе системы, в которой возникла проблема.
- Представьте, что вы ежедневно гуляете в этом парке, отдыхаете на берегу пруда под тенью вековых деревьев… Представьте себя в образе векового дерева… В образе птицы, живущей на этом дереве …
Учащиеся вовлекаются в дискуссию, итогом которой становится формулирование рационального условия для достижения поставленной цели: необходимо сохранить уникальные деревья.
После нахождения рационального условия, задача преобразуется следующим образом: Поверхность пруда имеет форму квадрата. В вершинах квадрата на берегу пруда растут четыре вековых уникальных дуба. Хотят вдвое увеличить площадь поверхности пруда, но так, чтобы новый пруд сохранил форму квадрата и все четыре дуба остались целы (т.е. были на берегу). Как это сделать?
Следующим этапом является переформулирование задачи и построение математической модели. Учитель предлагает заменить реальные объекты геометрическими (пруд – квадрат, дубы – точки) и построить чертеж. В диалоге формулируется соответствующая математическая задача: Дан квадрат АВСD. Построить квадрат, площадь которого в два раза больше площади данного квадрата, так, чтобы точки А, В, С, D лежали на его сторонах.
Организуется групповая работа над решением задачи. Учитель координирует работу учеников в группах, помогает найти идею решения. В каждой группе возможен свой способ (метод решения).
Далее организуется презентация решений групп. Учитель представляет свое решение на слайде (рис. 3). В ходе дискуссии выбирается наиболее рациональное решение.
Построим точки О1, O2, O3, O4, симметричные точке О относительно прямых АВ, ВС, CD и АD соответственно.
Докажем, что
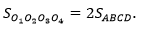
Пусть AB = х. Тогда площадь пруда равна х2. Площадь нового пруда 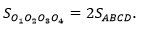 = 1/2 O1O3 · O2O4 = 2 x2.
= 1/2 O1O3 · O2O4 = 2 x2.

Завершается урок рефлексией, которую можно организовать с помощью опроса, созданного в онлайн сервисе Online Test Pad.
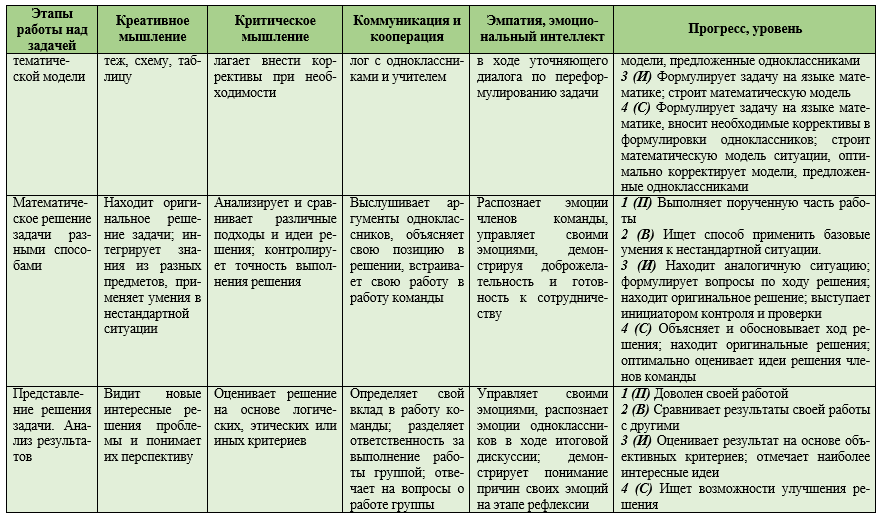
Научные результаты и дискуссия (ResearchResultsandDiscussion). Оценивание и мониторинг развития навыков “soft skills” осуществляется в ходе наблюдения за деятельностью учащихся по решению открытой практико-ориентированной задачи, при этом основной диагностический инструментарий учителя – это критериальная оценочная рубрика (табл. 2) и лист наблюдений (табл. 3).
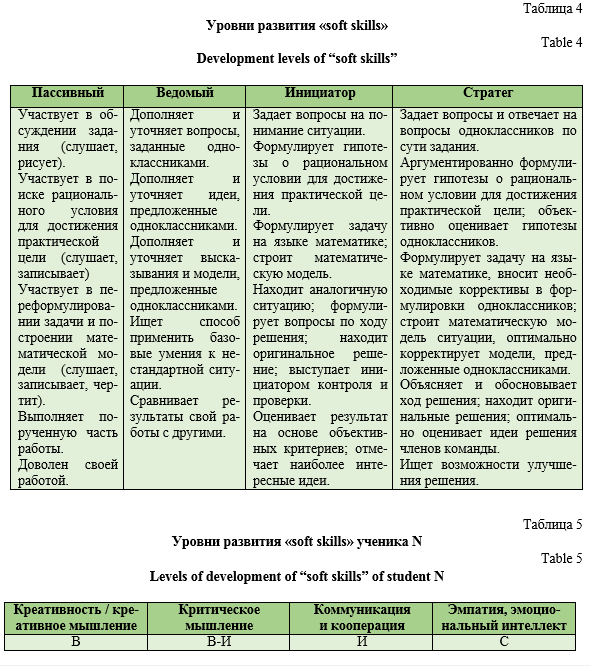
В табл. 2 даны общие описания компонентов навыков и характеристика уровней их сформированности на каждом этапе работы. Для понимания изменений, происходящих при переходе на более высокий уровень, необходимо учитывать, что все компоненты, проявившиеся на предыдущем уровне, сохраняются и служат основой для компонентов более высокого порядка. Общая логика прогресса развития навыков “soft skills” – это наращивание инициативности и самостоятельности, которые
проявляет ученик при решении открытой задачи. Условное обозначение уровней: 1 – «Пассивный» (П), 2 – «Ведомый» (В), 3 – «Инициатор» (И), 4 – «Стратег» (С), – отражает характер этого перехода и опирается на наблюдение за тем, как ученики проявляют себя в ходе групповой работы
(табл. 4).
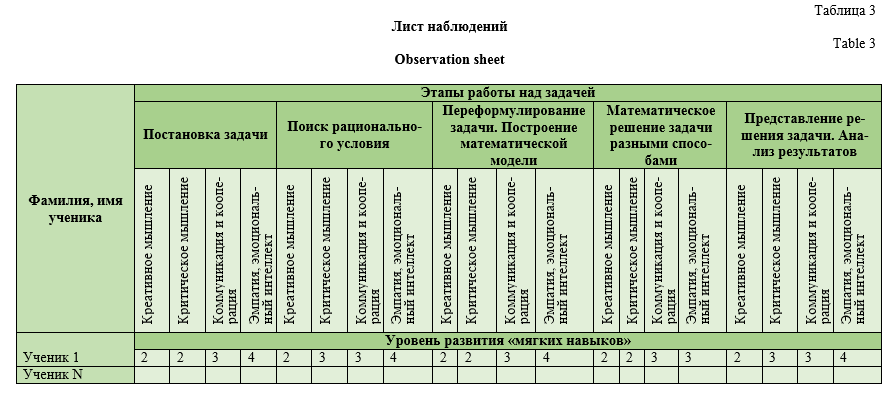
В листе наблюдений учитель фиксирует проявленный уровень развития “мягких навыков” на всех этапах решения задачи, после чего ставится оценка сформированности указанных навыков. Так, например, ученик N на всех этапах работы над задачей продемонстрировал второй уровень развития креативного мышления (В); на трех этапах из пяти – второй уровень развития критического мышления (В) и на двух этапах из пяти – третий уровень развития критического мышления (И); коммуникация и кооперация на всех этапах зафиксированы на третьем уровне (И); эмпатия и эмоциональный интеллект − на четвертом уровне (С)
(табл. 3). Тогда уровни развития “soft skills” такого ученика отражены в табл. 5:

Такая методика помогает проследить динамику изменений уровней развития «мягких навыков», кроме того, использование непараметрических методов статистики, а именно, биномиального критерия, позволяет проверить гипотезу об эффективности применяемой технологии открытых задач.
Биномиальный критерий (критерий знаков) – это непараметрический метод (применяемый для обработки качественных данных), позволяющий легко проверить, повлияла ли независимая переменная на выполнение задания испытуемыми. При это методе сначала подсчитывают число испытуемых, у которых результаты повысились (снизились), а затем сравнивают его с тем числом, которого можно было ожидать на основе чистой случайности. Далее определяют разницу между этими двумя числами, чтобы выяснить, насколько она достоверна.
При подсчетах результаты, свидетельствующие о повышении эффективности, берут со знаком плюс, а о снижении – со знаком минус; случаи отсутствия разницы не учитывают.
Расчет ведется по формуле:

где Х – сумма “плюсов” или сумма «минусов»;
n/2 – число сдвигов в ту или другую сторону при чистой случайности
0,5 – поправочный коэффициент, который прибавляют к Х, если Х< n/2, или вычитают, если Х >n/2 (Годфруа, 1992).
Рассмотрим результаты, полученные в экспериментальной группе по каждому из выделенных “soft skills” (количество испытуемых n=20) (табл. 6).
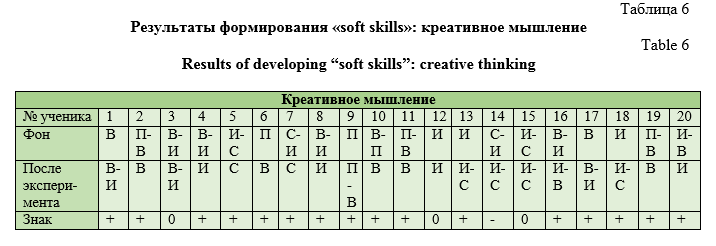

Так как 1,74>1,64, то принимаем гипотезу об эффективности технологии открытых задач при обучении математике для развития креативного мышления.
Аналогично анализируются результаты по другим “мягким навыкам”. Таким образом, подтверждаются гипотезы об эффективности рассматриваемой технологии для развития критического мышления (Z=1,76), коммуникации и кооперации (Z=1,79), эмпатии и эмоционального интеллекта (Z=1,78).
Заключение (Conclusions). Таким образом, спроектирована модель формирования “soft skills” на основе открытых практико-ориентированных задач при обучении математике. Данная модель детализирует деятельность ученика и учителя на каждом этапе работы над задачей, конкретизируя методы и формы работы, а также структуру и содержание «мягких навыков», критического мышления, креативности, коммуникации и кооперации, эмпатии и эмоционального интеллекта. Модель предусматривает наблюдение динамики развития и процедуру оценивания указанных навыков. С целью проверки эффективности спроектированной модели был проведен пилотный эксперимент среди учащихся девятого класса в количестве двадцати человек. По результатам исследования сделаны следующие выводы:
1) спроектированная модель формирования «мягких навыков» на основе открытых практико-ориентированных задач является достаточно эффективным средством развития и совершенствования “soft skills” при обучении математике;
2) указанная модель может быть использована как инструмент измерения уровней развития «мягких навыков», однако необходимо учесть то обстоятельство, что в качестве способа измерения используются оценки учителя, а значит, не исключена возможность субъективной оценки;
3) возможно усовершенствование процесса мониторинга развития “soft skills” с помощью объективных процедур оценивания, например, таких, как компьютерное тестирование, куда будут включены задания на определение уровня развития выделенных составляющих «мягких навыков»: креативности, критического мышления, коммуникации и кооперации, эмпатии и эмоционального интеллекта.
[1] 10 Top Soft Skills for 2020: What They Are and How To Train Them, 2016. URL: https://www.game-learn.com/top-soft-skills-2020-how-to-train-them/ (дата обращения: 25.03.2021).
[2] 4К: измерение критического мышления, креативности, коммуникации и кооперации, 2021. URL: https://ioe.hse.ru/monitoring/4k (дата обращения: 25.03.2021).


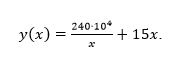

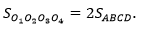
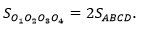 = 1/2 O1O3 · O2O4 = 2 x2.
= 1/2 O1O3 · O2O4 = 2 x2.
























Список литературы